티스토리 뷰
정렬 알고리즘 중에 하나인 힙 소트(Heapsort)에 대해 알아보자.
힙 소트는 힙을 이용하여 정렬하는 알고리즘이다.
힙(heap)이란 무엇을 의미할까?
C언어를 좀 깊게 파봤다면 메모리 영역 중에 힙 영역이란 말을 들어 봤을 것이다.
하지만 여기서 말하는 힙은 그 힙이 아니다.
여기서 말하는 힙이란 완전 이진트리(complete binary tree)를 기반으로 하는 자료구조로
최댓값 또는 최솟값을 빠르게 찾기 위해 힙 속성이라는 것을 갖고 있다.
(출처 : ko.wikipedia.org/wiki/%ED%9E%99_(%EC%9E%90%EB%A3%8C_%EA%B5%AC%EC%A1%B0))
완전 이진트리는 en.wikipedia.org/wiki/Binary_tree#Types_of_binary_trees에 잘 설명되어 있다.
쉽게 말하자면 자식 노드를 최대 2개까지 가질 수 있는 트리가 이진트리이고
이진트리의 마지막 레벨을 제외한 다른 레벨들은 노드들로 가득 차있고
마지막 레벨은 왼쪽부터 오른쪽 방향으로 노드들이 채워져 있어야 완전 이진트리가 된다.
그리고 완전 이진트리의 각 노드에 키 값이 존재하고
부모 노드의 키 값이 자식 노드들의 키 값보다 항상 크거나 같은 속성을 가지면 최대 힙(max-heaps)이라 부르고
부모 노드의 키 값이 자식 노드들의 키 값보다 항상 작거나 같은 속성을 가지면 최소 힙(min-hepas)라고 부른다.
아래 그림은 최대 힙의 예시이다.

위 그림과 같이 힙은 보통 배열로 나타낸다.
트리에 있는 키 값들을 위에서부터 왼쪽에서 오른쪽으로 차례대로 배열에 저장하면 된다.
그러면 어떤 노드의 배열 인덱스에서 1을 빼고 2로 나누면 그 노드의 부모 노드 인덱스가 되고 (루트 노드 제외)
2를 곱하고 1을 더하면 왼쪽 자식 노드의 인덱스가, 1을 더하고 2를 곱하면 오른쪽 노드의 인덱스가 된다.
우리는 이 힙을 정렬하는데 사용할 것이다.
최대 힙과 최소 힙은 원리가 똑같으니 최대 힙에 대해서만 설명하도록 하겠다.
최대 힙을 사용하여 정렬하기 위해서 우리에게 필요한 작업은 두 가지가 있다.
첫 번째로 임의의 순서로 키 값들이 나열되어 있는 배열을 입력받고 이것을 최대 힙으로 만든다.
두 번째로 최대 힙을 사용해서 정렬한다.
위 두 가지 작업을 하기 위해서 힙 속성을 만족시키게 하는 Heapify 함수를 정의해 보자.
이 함수는 이미 최대 힙 속성을 만족하고 있는 힙에서 임의의 노드의 키 값이 변경되었을 때
다시 힙 속성을 맞춰주기 위한 함수로 생각하면 이해하기 쉽다.
typedef int Element;
class MaxHeap
{
protected:
std::vector<Element> _elements;
void exchange(Element& element1, Element& element2)
{
Element temp = element1;
element1 = element2;
element2 = temp;
}
public:
void Heapify(std::size_t idx, std::size_t size)
{
std::size_t largest = idx;
std::size_t left = idx * 2 + 1;
std::size_t right = (idx + 1) * 2;
if (size > left && _elements[idx] < _elements[left])
{
largest = left;
}
if (size > right && _elements[largest] < _elements[right])
{
largest = right;
}
if (idx != largest)
{
exchange(_elements[idx], _elements[largest]);
Heapify(largest, size);
}
}
};
위의 Heapify 함수에서 부모 노드와 왼쪽 자식 노드, 오른쪽 자식 노드 중에서 키 값이 가장 큰 노드를 찾고
그 노드가 부모 노드가 아니면 부모 노드와 키 값을 교환하고 다시 그 노드에 대해서 Heapify 함수를 호출한다.
먼저 세 개 노드 중에서 부모 노드에 가장 큰 키 값을 놓도록 한다.
이것은 앞서 설명한 최대 힙의 속성을 만족시키도록 만든다.
그리고 키 값이 바뀐 노드가 부모 노드로서 최대 힙 속성을 만족시키도록 그 노드에 대해 Heapify 함수를 호출해 준다.
정리해보면 최대 힙 속성을 만족시키는 힙에서 임의의 노드의 키 값이 변경되었을 때
그 키 값이 위치할 적당한 노드를 찾아 이동시키는 작업이 된다.
이 작업을 가장 끝 노드에서부터 루트 노드까지 반복하면
즉, 배열의 끝에 있는 요소부터 첫 번째에 있는 요소까지 Heapify 함수를 호출해 주면
우리가 하려는 첫 번째 작업인 임의의 순서로 키 값들이 나열된 배열을 최대 힙으로 만드는 작업이 완료된다.
이 작업을 아래와 같이 Build 함수로 정의해 보자.
typedef int Element;
class MaxHeap
{
protected:
std::vector<Element> _elements;
void exchange(Element& element1, Element& element2)
{
...
}
public:
void Heapify(std::size_t idx, std::size_t size)
{
...
}
void Build()
{
if (1 >= _elements.size())
{
return;
}
const std::size_t size = _elements.size();
std::size_t idx = size / 2 - 1;
while (0 <= idx)
{
Heapify(idx, size);
if(0 == idx)
{
break;
}
else
{
idx--;
}
}
}
};
앞서 마지막 노드부터 Heapify 함수를 호출해 준다고 했지만
자식 노드가 없는 리프 노드(leaf node)들은 Heapify 함수를 호출해 줄 필요가 없다.
왜냐하면 부모 노드 하나만 존재하고 항상 최대 힙 속성을 만족시키기 때문이다.
따라서 리프 노드들이 아닌 노드부터 루트 노드까지 Heapify 함수를 호출해 주면 된다.
(리프 노드가 아닌 마지막 노드의 인덱스는 총 노드 개수 / 2 - 1로 구할 수 있다.
참고 : ita.skanev.com/06/01/07.html)
Build 함수가 왜 임의의 순서로 키 값들이 나열된 배열을 최대 힙으로 만들 수 있는지는 곰곰이 생각해 보자.
이해를 돕기 위해 아래와 같이 간단한 예시를 확인해 보자.
위 그림은 임의의 순서로 키 값들이 나열된 초기 상태의 배열과 트리로 표현한 것이다.
다음 그림들은 위 배열에 대해 Build 함수를 호출할 때의 과정을 나타낸다.
빨간색으로 표시한 숫자는 Build 함수에 있는 idx를 나타낸다.
그리고 파란색으로 표시한 숫자는 Heapify 함수에 의해 교환된 키 값들을 나타낸다.




위의 마지막 그림은 맨 처음 소개한 최대 힙과 다른 모습이긴 하지만 이것 또한 최대 힙 속성을 만족하므로 최대 힙이다.
순서대로 잘 살펴보면 어떤 노드에 대해 Heapify 함수를 호출하기 전에
그 노드의 자식 노드들에 대해서 먼저 Heapify 함수가 호출되는 것을 확인할 수 있다.
즉, 각 노드를 루트 노드로 하는 서브 트리(subtree)들을 모두 최대 힙으로 만들면서
마지막으로 루트 노드에 대해서 최대 힙을 만들고 배열 전체를 최대 힙으로 만들게 된다.
이제 두 번째 작업으로 이 힙을 이용하여 배열에 있는 키 값들이 오름차순이 되도록 정렬해 보자.
방법은 최대 힙에서 최댓값인 루트 노드의 키 값과 최대 힙의 마지막 요소의 키 값을 교환한 후
최대 힙의 길이를 1 감소시키고 루트 노드에 대해 Heapify 함수를 호출한다.
이 작업을 최대 힙 길이가 1이 될 때까지 반복한다.
아래와 같이 Sort 함수로 정의해 보자.
typedef int Element;
class MaxHeap
{
protected:
std::vector<Element> _elements;
void exchange(Element& element1, Element& element2)
{
...
}
public:
void Heapify(std::size_t idx, std::size_t size)
{
...
}
void Build()
{
...
}
void Sort()
{
if (1 >= _elements.size())
{
return;
}
std::size_t size = _elements.size();
while (1 < size)
{
exchange(_elements[0], _elements[size - 1]);
size--;
Heapify(0, size);
}
}
};
위에서 봤던 최대 힙 기준으로 정렬되는 모습을 차례대로 살펴보자.
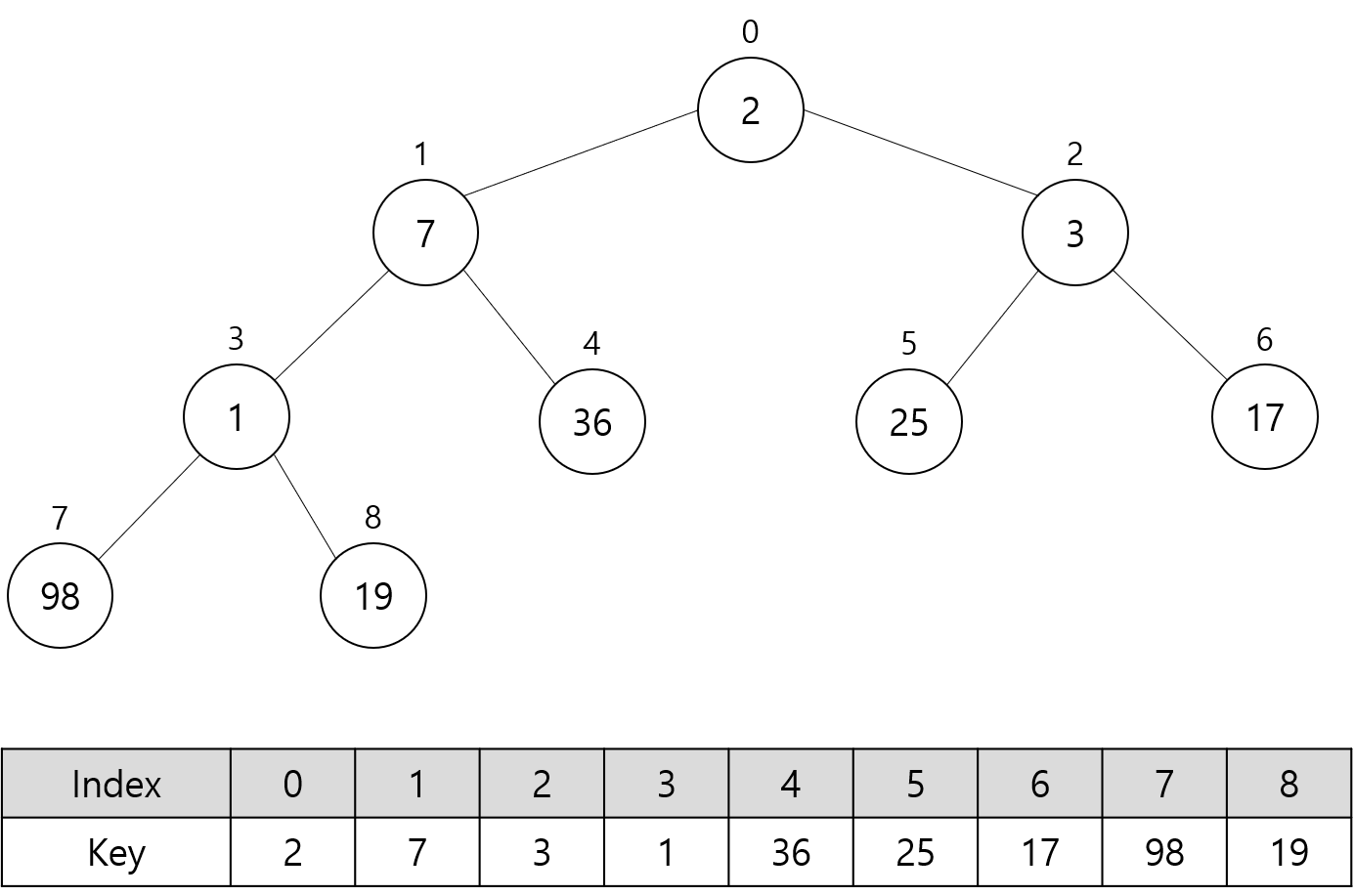
초기 최대 힙은 아래와 같다.

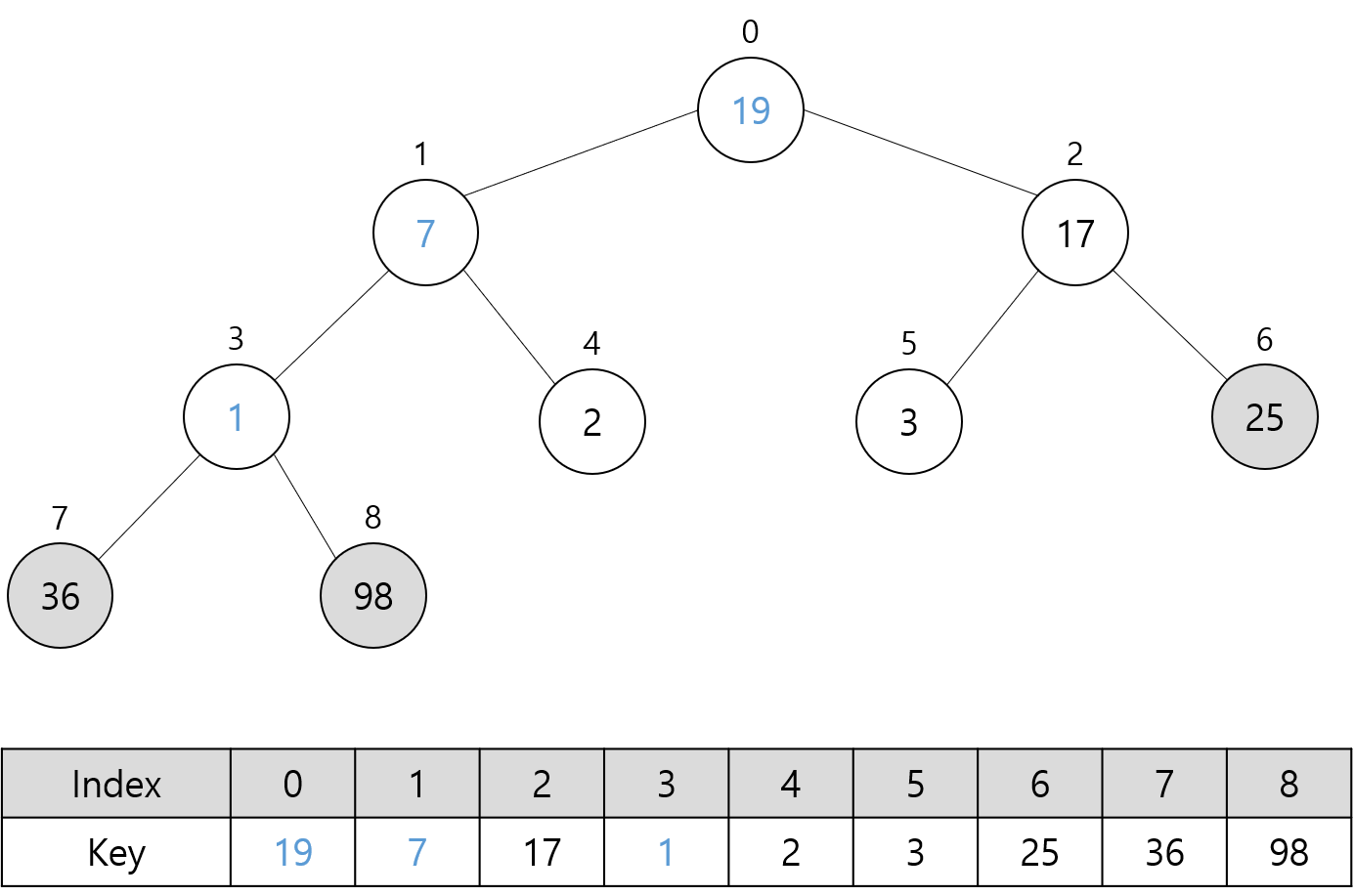
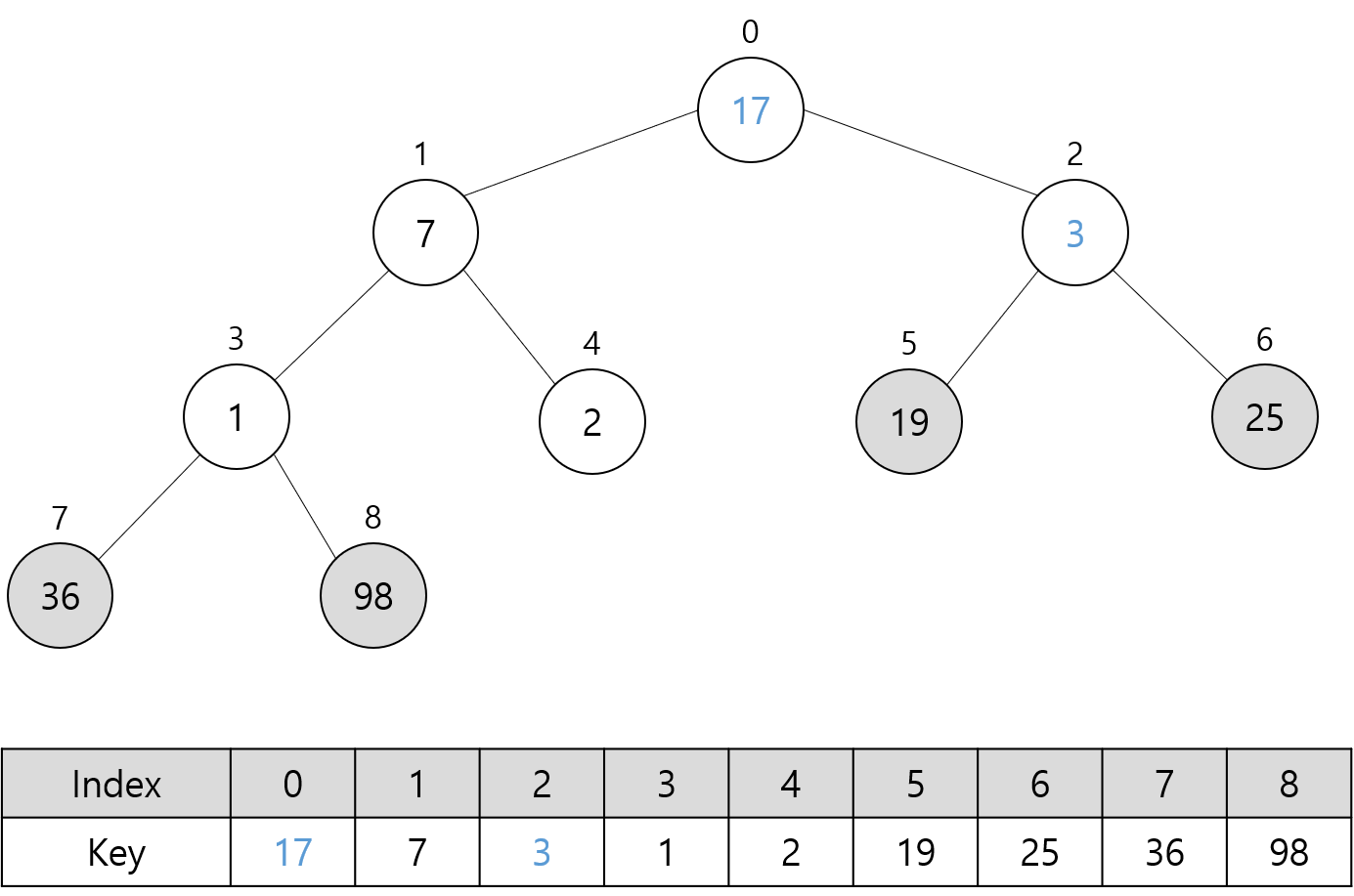
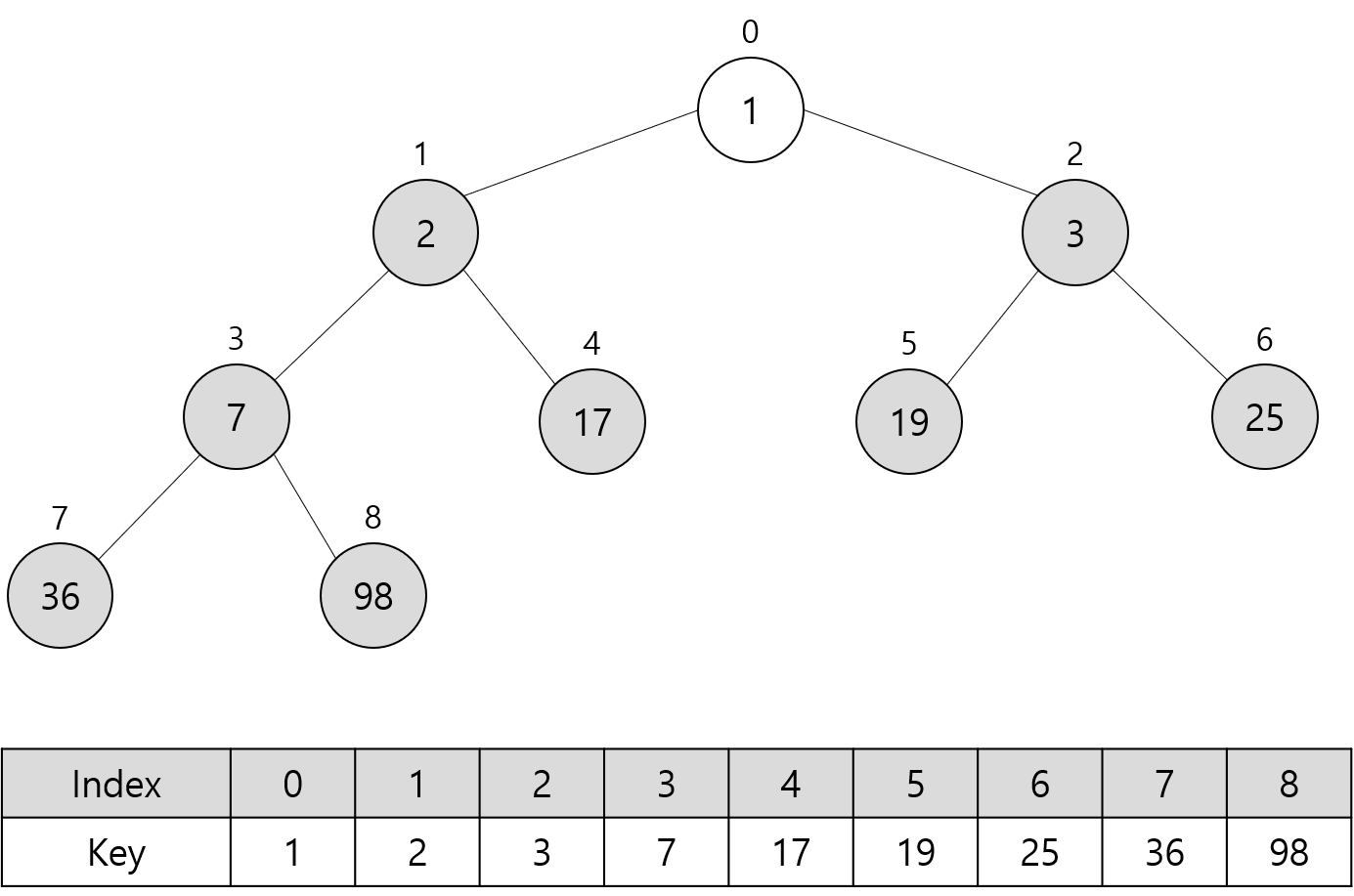
다음 그림들은 위 최대 힙에 대해 Sort 함수를 호출할 때의 과정을 나타낸다.
트리에서 회색으로 채운 노드는 최대 힙에 포함되지 않는 노드를 의미한다.
파란색으로 표시한 숫자는 루트 노드에 대해 Heapify 함수 호출로 교환된 키 값들을 나타낸다.





이제 힙 소트의 시간 복잡도와 공간 복잡도에 대해서 알아보자.
총 노드 개수를 n이라고 하자.
먼저 힙 소트의 공간 복잡도는 $O(1)$이 된다.
힙 소트는 in-place 알고리즘으로 입력 크기에 관계 없이 상수 크기만큼의 공간을 추가로 필요하기 때문이다.
(in-place algorithm : en.wikipedia.org/wiki/In-place_algorithm)
시간 복잡도는 함수 별로 조사해 보자.
먼저 Heapify 함수를 실행하는 특정 노드의 높이를 h라고 했을 때
그 노드의 Heapify 함수의 실행 시간은 $O(h)$라고 할 수 있다.
(리프 노드까지 도달할 때 제일 오래 걸리므로)
그렇다면 높이 0부터 (리프 노드의 높이가 0) 높이 $\lfloor\log_{2}n\rfloor$까지 차례대로
각 높이에 있는 노드 개수와 Heapify 함수의 실행 시간 $O(h)$를 곱한 값을 모두 더하면
Build 함수의 시간 복잡도를 구할 수 있다.
식으로 표현하면 아래와 같다.
$$\sum_{h=0}^{\lfloor \log_{2}n \rfloor} \lceil {n \over 2^{h+1}} \rceil O(h) = O(n \sum_{h=0}^{\lfloor \log_{2}n \rfloor} {h \over 2^{h}})$$
$\lceil {n \over 2^{h+1}} \rceil$은 높이 h에 있는 노드의 최대 개수이다.
(자세한 내용은 ita.skanev.com/06/03/03.html 참고)
그리고 아래와 같은 공식이 있다.
$$ \sum_{k=0}^{\infty} kx^{k} = { x \over (1 - x)^{2} } \quad for \mid x \mid < 1 $$
위 공식을 사용하여 $x = 1/2$를 대입하면 아래와 같이 식이 성립한다.
$$ \sum_{h=0}^{\infty} { h \over 2^{h} } = { 1/2 \over (1 - 1/2)^{2} } = 2 $$
총 노드 개수 n이 무한히 크다고 가정하고 위의 식을 적용하면 아래와 같다.
$$ O(n \sum_{h=0}^{\lfloor \log_{2}n \rfloor} { h \over 2^{h} }) = O(n \sum_{h=0}^{\infty} {h \over 2^{h}}) = O(n) $$
따라서 Build 함수는 $O(n)$으로 선형 시간(linear time) 복잡도를 가진다.
마지막으로 Sort 함수의 시간 복잡도를 알아 보자.
루트 노드에 있는 키 값을 마지막 노드의 키 값과 교환하는 작업을 n번 수행한다.
그리고 매번 Heapify 함수를 호출하는데 Heapify 함수의 시간 복잡도를 아래와 같이 정의할 수 있다.
$$ T(n) \; \leq \; T({2n \over 3}) + \Theta(1) $$
Heapify 함수에서 노드들끼리 키 값을 교환하는 작업이 $\Theta(1)$이고
키 값을 교환하고 자식 노드에 대해서 다시 Heapify 함수를 호출할 때
최대 $T({2n \over 3})$의 실행 시간이 걸린다.
이는 최악의 경우 노드 개수 비율이 한쪽 자식 노드 개수가 다른 한쪽 자식 노드 개수보다 2배 많다는 뜻이다.
이를 쉽게 말하자면 트리의 마지막 레벨에 한쪽 자식 노드 쪽에는 노드들이 가득 차 있고
다른 한 쪽 노드 쪽에는 비어 있는 케이스이다.
예를 들어 아래와 같이 표현할 수 있다.

회색 노드가 현재 Heapify 함수가 호출된 대상 노드이다.
(어떠한 서브 트리의 루트 노드일 수 있다.)
그리고 파란색 노드가 다시 Heapify 함수가 호출된 자식 노드라고 하자.
파란색 노드가 루트 노드인 서브 트리 기준으로 리프 노드 개수와 리프 노드가 아닌 노드들의 개수는 거의 같다.
(참고 : ita.skanev.com/06/01/07.html)
파란색 노드 기준의 서브 트리에서 리프 노드를 제외하면 반대쪽 자식 노드의 개수와 같으므로
파란색 노드 기준의 서브 트리의 노드 개수가 회색 노드 기준의 서브 트리 노드 개수의 ${2 \over 3}$ 비율을 차지한다.
고로 위와 같은 부등식이 성립하고 마스터 정리(master theorem)로 $T(n) = O(\log_{2}n)$임을 알 수 있다.
(en.wikipedia.org/wiki/Master_theorem_(analysis_of_algorithms))
따라서 Sort 함수의 총 시간 복잡도는 $O(n\log_{2}n)$이 되고
힙 소트의 총 시간 복잡도는 $ O(n) + O(n\log_{2}n) = O(n\log_{2}n)$이 된다.
여기까지 힙 소트에 대해서 알아 보았다.
내용 출처 : Introduction to Algorithms (en.wikipedia.org/wiki/Introduction_to_Algorithms)
'알고리즘 > study' 카테고리의 다른 글
| 우선순위 큐 (Priority Queue) (0) | 2021.04.11 |
|---|---|
| [분할 정복] Strassen algorithm (0) | 2020.11.26 |
| 문자열 검색 알고리즘 2편 (Boyer Moore) (0) | 2020.04.19 |
| 문자열 검색 알고리즘 1편 (Naive, Rabin Karp, KMP) (1) | 2020.04.16 |
| [그래프] 최단 경로 알고리즘 (Shortest path algorithms) (0) | 2019.12.08 |
- Total
- Today
- Yesterday
- operating system concepts
- red black tree
- minimum spanning tree
- Prim
- boyer moore
- divide & conquer
- Kruskal
- leetcode
- Dijkstra
- 레드블랙트리
- Introduction to Algorithms
- Longest Palindromic Substring
- rabin karp
- 최소 신장 트리
- heapsort
- Strassen algorithm
- 퀵 소트
- Median of Two Sorted Arrays
- Shortest path
- 최단 경로 알고리즘
- 힙 소트
- KMP
- quick sort
- strassen
- 문자열 검색 알고리즘
- 최단 경로
- string searching algorithm
- 퀵소트
- 플로이드
- 레드 블랙 트리
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
